Advanced proton beam dosimetry part II: Monte Carlo vs. pencil beam-based planning for lung cancer
Introduction
Proton pencil beam scanning (PBS) is an advanced delivery mode of proton therapy which is used to effectively treat a multitude of oncologic disease sites (1). Lung cancer, particularly in the setting of locally advanced disease, is increasingly treated with PBS and presents many technical challenges during treatment planning, including respiratory motion-induced interplay effects (2,3) as well as tissue density heterogeneities within and proximal to the target volume (4). Traditionally, standard-of-care treatment planning for lung lesions with proton therapy has relied on analytical pencil beam (PB) dose calculation algorithms (5) across commercial treatment planning platforms. Many of these PB analytical algorithms are based on the works of Hong et al. (6) and Schaffner et al. (7), which offer fast and efficient computation but come at the cost of reduced proton beam dose calculation accuracy in the presence of complex geometries comprised of heterogeneous tissue interfaces (8). Variations in dosimetry from different proton therapy dose calculation algorithms can have downstream effects on tumor control probability and normal tissue complication rates (9).
Recently, RaySearch Laboratories (Stockholm, Sweden) released a Monte Carlo (MC) dose calculation algorithm RayStation version 6.0TM (RS6) treatment planning system (10). The inclusion of MC in commercial treatment planning systems beyond in-house solutions (11) opens the door for clinical use and offers the promise of increased accuracy in dose calculation for complex disease sites such as lung lesions. Previous studies on MC dosimetry for small proton fields (12), as well as comparisons of PB versus MC dosimetry, have been limited to dose calculation in phantoms (13-16). Investigators characterized a range of dose calculation errors for different phantom materials and geometric configurations, but did not explicitly evaluate dosimetric effects on clinical patient data. Increased understanding of the impact of MC-based clinical treatment planning for lung cancer patients relative to PB-based planning could reveal key tradeoffs in plan quality and establish realistic goals for proton dosimetry.
Advanced Proton Beam Dosimetry Part I provided a review of the PB and MC proton dose calculation algorithms and presented examples of dose differences in heterogeneous phantoms. In Part II of this series, we investigate MC-based PBS treatment planning for lung cancer patients by evaluating dose differences between RS6 PB and RS6 MC algorithms. The retrospective analysis of ten lung cancer patients treated with PBS addresses the following points: (I) difference in dose to targets and organs at risk (OARs) when PB-optimized (PBopt) treatment plans are re-calculated with MC; (II) difference in dose to targets and OARs between PBopt and MC-optimized (MCopt) treatment plans; and (III) difference in robustness to setup and range uncertainties between MC-calculated perturbed treatment plans and MC-optimized perturbed treatment plans.
Methods
Patient cohort
Following approval from the Institutional Review Board at the University of Washington, treatment planning data from ten patients diagnosed with lung cancer who received definitive proton PBS thoracic therapy were reviewed and analyzed. Five patients presented with a variety of etiologies (small/non-small cell lung cancer), stages II–III, and treatment modality combinations (adjuvant radiation, concurrent chemoradiation). The remaining five patients were prospectively enrolled onto a phase I/II trial (NCT02773238) of functional lung avoidance (17) with strict eligibility criteria: stage IIB–IIIB non-small cell lung cancer, ECOG 0-1, radiation and chemotherapy naïve, concurrent chemoradiation to at least 60 Gy [relative biological effectiveness (RBE)] in 30 fractions, and standards for lung, liver, and renal function. Across all ten patients, tumor volumes ranged from 81 to 637 cc with a median of 261 cc and all treatment targets contained regions of heterogeneity characterized by lung-tissue interfaces.
Simulation technique
Patient treatment simulation was performed through a free-breathing acquisition of 4D computed tomographic (4DCT) images on a GE Optima CT580 scanner (GE Healthcare, Waukesha, WI, USA) with 120 kVp, variable tube current, and 2.5 mm slice thickness technique. Respiratory traces were recorded by the AZ 733V Respiratory Gating SystemTM (Anzai Medical Co. Ltd., Tokyo, Japan) platform consisting of a pressure sensor belt. 4DCT data were binned into ten equally spaced phases across the patient respiratory cycle. The total vector target motion was evaluated to be less than 1.0 cm in all cases, and did not require further motion mitigation strategies such as abdominal compression. Rather, a motion-encompassing treatment planning strategy was employed via construction of an internal target volume in combination with volumetric rescanning (18) to dampen the interplay between scanning magnet motion and tumor motion frequencies.
Treatment planning and optimization parameters
DICOM CT data were imported into RS6 and PBS treatment plans were optimized for dose calculation on 4DCT phase-averaged images. PBS gantry treatment plans of 1–2 beams (2–4 beams with 2× volumetric rescanning) were generated using single-field robust optimization to maintain target coverage under perturbed conditions of 3% range and 3 mm setup uncertainty. Prescriptions consisted of definitive proton beam therapy regimens with curative intent, ranging from 60–66.6 Gy (RBE) in 1.8–2.0 Gy (RBE) per fraction using an average RBE of 1.1. Additional beam computation settings used for PB and MC optimization included RS6 default energy layer spacing and spot spacing parameters based on energy-dependent pristine Bragg peak width and energy-dependent spot size. A lateral margin of up to 1.0 cm was used for spot placement around the target and all optimizations were carried out on a 2 mm calculation grid for 200 iterations (nominal). A sampling history of 10,000 ions/spot was enforced for MC optimization and final MC dose was computed using a sufficient number of ions to yield 0.5% statistical uncertainty across the target. All PB and MC plans were normalized such that the prescribed dose covered 95% of the planning target volumes.
Dosimetric and statistical analysis
PBS single field optimization was first carried out using RS6 PB v4.0 (PBopt) to achieve clinical goals for target coverage and dose to OAR in compliance with the current standard of care. PBopt treatment plans were then re-calculated using RS6 MC v4.0 [MC-recalculated (MCrecalc)] without modification to PBS energy layers, spot positions, and spot intensity distributions. Lastly, while maintaining the same optimization parameters and field-specific energy layers, spot positions and spot intensities were reset and re-optimized using RS6 MC v4.0 (MCopt). Dose differences between PBopt, MCrecalc and MCopt treatment plans were recorded for the following plan metrics: clinical target volume (CTV) V95, CTV homogeneity index (HI), total lung V20, total lung VRX (relative volume of lung receiving the prescribed dose or higher), and global maximum dose. Pairwise differences in planned dose and dose-volume parameters between PBopt, MCrecalc, and MCopt were evaluated with a non-parametric Friedman test.
Perturbed dose distributions were generated for the evaluation of treatment plan robustness to setup and range uncertainties. Perturbation scenarios consisted of under/over-ranging beams by scaling the CT density by +/−3% and shifting beam isocenters +/−3 mm in the medial/lateral (x), superior/inferior (y) and anterior/posterior (z) directions. For simplicity, two representative worst-case dose perturbations scenarios were defined under the following conditions: +3%, x+3 mm, y+3 mm, z+3 mm and −3%, x−3 mm, y−3 mm, z−3 mm. Perturbed doses were generated for MCrecalc and MCopt treatment beams. Pairwise differences between MCrecalc and MCopt perturbed dose distributions were evaluated with a non-parametric Wilcoxon sign-rank test.
Results
Figure 1 illustrates isodose distributions overlaid on a patient planning CT under three planned dose conditions: PBopt (A), MCrecalc (B) and MCopt (C). Tissue inhomogeneity increases the spread in range from the posterior beam direction in the MCrecalc dose distribution (B), which has the effect of pulling isodose lines back (i.e., decreasing range) through bone/tissue/air. Dose shadowing of proton beam paths beyond bone is more pronounced in MCrecalc (B) compared to PBopt (A). This under-ranging is corrected in the MCopt plan (C), though the distal edge features more lateral dose inhomogeneity than the PBopt plan (A). Figure 1D is a plot of the corresponding DVH for the CTV (green) and lung (blue). There is a substantial drop in CTV coverage in the MCrecalc plan (dotted line) that is recovered in the MCopt plan (dashed line), while no significant differences in lung dose-volume histogram (DVH) are observed. Figure 1E shows a line dose profile across the center of the target for the three treatment plans. While there is reasonable dosimetric agreement at the level of the patient midplane (i.e., mediastinum), there is lower dose through the tissue/air interface in the MCrecalc profile (dotted line) compared to the PBopt (solid line) and MCopt (dashed line) profiles.
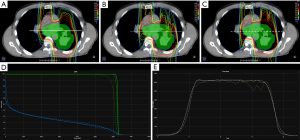
Table 1 lists dose differences to the total lung and CTV between the PBopt, MCrecalc and MCopt treatment plans. In this ten-patient sample, CTV V95 ranged from 99% to 100% with a median of 100% for PBopt plans. Under MCrecalc, CTV V95 ranged from 77% to 94% with a median of 90%, which was a statistically significant drop in target coverage relative to PBopt (P<10−5). Under MCopt, CTV V95 ranged from 99% to 100% with a median of 100%, constituting a significant recovery in target coverage (P<10−5). MC treatment plans showed a reduction of dose homogeneity within the target volume. The median CTV HI (D95/D5) was 0.98 for PBopt, 0.91 for MCrecalc and 0.95 for MCopt (P<10−3). Total lung V20 distributions were not statistically different among dose calculation and optimization scenarios, with median V20 within 2% between PBopt (25%), MCrecalc (25%) and MCopt (27%), P=0.27. Median lung VRX (i.e., percentage of lung receiving prescription dose or higher) was 7%, 1% and 8% for PBopt, MCrecalc and MCopt, respectively (P<10−3), indicating a reduction in lung volume receiving high dose when recalculated with MC. Lastly, the global maximum patient dose increased from a median value of 106% for PBopt to 109% and 112% for MCrecalc and MCopt, respectively (P<10−3), for fixed levels of MC statistical uncertainty.
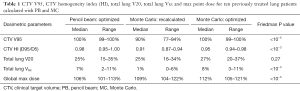
Full table
Given the inaccuracies of PB dosimetry, summarized numerically in Table 1, robustness evaluation was restricted to plans utilizing MC dosimetry. Table 2 shows delta values representing the change in CTV D95 and global max dose for MCrecalc and MCopt treatment plans following range and isocentric setup perturbations: +3% density/under-range, x+3 mm, y+3 mm, z+3 mm and −3% density/over-range, x−3mm, y−3mm, z−3mm. Median change under perturbation in CTV D95 was −6% and −1% for MCrecalc and MCopt plans, respectively, which represented a statistically significant improvement in plan robustness when optimizing with MC (P=0.006). Change in global maximum dose under perturbation was not statistically different between MCrecalc and MCopt plans (P=0.100), suggesting that this parameter was most influenced by statistical noise present in both planning scenarios.
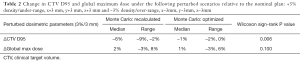
Full table
Discussion
Advanced Proton Beam Dosimetry Part I demonstrated that analytic algorithms lack proton dose calculation accuracy in highly heterogeneous tissues typically encountered during the treatment of lung cancer. Saini et al. (16) benchmarked the RS6 PB and MC dose calculation algorithms with measurements and found that MC provided superior accuracy, especially in heterogeneous media. Similarly, Lin et al. (19) benchmarked the Eclipse Acuros PTTM (Varian Inc., Palo Alto, CA, USA) MC algorithm. In this clinical planning study, analysis of lung cancer patient treatment plans optimized with a commercial PB algorithm and subsequently recalculated with a commercial MC algorithm demonstrated a median decrease of 10% in CTV V95. These results are in line with recent findings by Taylor et al. (15), in which measurements from anthropomorphic lung phantom data concluded that use of analytic dose algorithms underdosed target centers by an average of 7%. Our recalculated MC planning results are likewise congruent with those of Schuemann et al. (20,21), in which they observed decreases of 11% in tumor control probability of lung cancer from MC dosimetry of analytic PB-optimized plans. While these investigations detailed the deficiencies in PB algorithms, they did not address the impact of MC-based optimization on planned dosimetry of lung cancer patients.
While a reduction in target dose was observed when recalculating with MC, CTV coverage under MC-based plan optimization was statistically similar to that achieved in the original PB-based optimization. This illustrates that when moving from PB to MC dosimetry, target coverage is lost but can be regained when MC optimization is used. A similar drop in dose homogeneity between PBopt (CTV HI =0.98) and MCrecalc plans (CTV HI =0.91) was observed. Unlike target coverage however, dose homogeneity is not fully restored when MC optimization is employed (CTV HI =0.95). Similar target coverage in lung lesions can be expected when optimizing with PB and MC with the caveat of reduced dose homogeneity under MC-based treatment planning.
Differences in normal lung tissue dosimetry were less pronounced for large volumes receiving low/moderate dose but similar in magnitude for small volumes receiving high dose compared to differences in target dosimetry. Total lung V20 remained within 2% deviation across the three dose calculation techniques, and similar trends were observed for V10 and V5 (data not shown). Dose differences in VRX exhibited a similar trend as CTV coverage across dose calculation techniques. Moving from PB to MCrecalc, VRX was reduced from 7% to 1% but increased back up to 8% under MC plan optimization. High-dose lung regions proximal to targets and tissue interfaces were most affected by differences in dose calculation algorithm. This trend held true for other OAR, though their nominal dosimetry was highly specific to patient anatomic geometry and tumor size/location (data not shown). For example, cases in which the spinal cord was a dose-limiting structure produced large variability in maximum dose between PB and MC algorithms.
Analysis of median global maximum dose showed an increase from 106% to 109% for PBopt and MCrecalc plans, and a further increase to 112% for MC-optimized plans. However, it should be noted that MC calculation statistical uncertainty can impact maximum point doses. As a fixed statistical uncertainty of 0.5% was used in this study, maximum dose may have been decreased further in some cases by shrinking statistical uncertainty. Increasing the simulated number of ions and their particle interaction histories can improve the precision of MC dose calculation at the expense of increased calculation time.
Unfavorable tradeoffs between dosimetric precision and computational efficiency have historically challenged the clinical adoption of MC-based proton therapy planning. Modern computing and parallelizable optimization on graphical processing units (GPU) recently opened the door to a new era of commercial MC proton therapy planning. Despite these advances, planning times for lung cancer treatments using MC optimization are typically 3–5 times longer than using PB optimization, and can exceed 10 times longer in duration for complex robust optimization scenarios. Continued advances in computational hardware and software to speed up optimization and dose calculation times are likely to diminish the impact of this treatment planning tradeoff in the near future.
Interestingly, robustness analysis revealed differences in perturbed dosimetry between MCrecalc and MC-optimized planning conditions. Plans that were robustly optimized with PB algorithms and recalculated with MC algorithm had a median change in CTV D95 of −6% under 3%/3 mm perturbed dose scenarios, while plans robustly optimized with MC algorithms had a negligible median change of −1%. This indicates that although robust optimization was employed in all dose calculations, treatment plans optimized with PB were more sensitive to range and setup uncertainty than plans optimized with MC. This is especially relevant for isocentric setup perturbations that are orthogonal to an air/tissue/bone interface for any beams directed parallel to the interface. Under these conditions, PBopt plans inaccurately estimate lateral dosimetry from an infinite slab approximation for each PB and consequently fail to build in robust margins, whereas MC-optimized plans account for this dosimetric uncertainty by accurately estimating lateral spread along the interface from individual particle interactions. Unlike target coverage, global maximum dose showed no difference between MCrecalc and MC-optimized plans, which suggests that the effect of robust optimization algorithm was smaller compared to the effect of statistical MC uncertainty on point doses.
Work presented in this study provided dosimetric evaluations of MC-based plans for lung proton PBS treatments. However, further analyses were constrained by several limitations. First, the cohort was limited to ten patients and future work in this area could be extended to a larger lung patient population, including subgroup analysis by disease stage, tumor location, magnitude of tumor motion, and beam configuration. Furthermore, while all patients in this study received definitive lung cancer proton beam therapy, the size and location of target volumes across the cohort varied substantially. This variation in target size and location caused a correspondingly high degree of variability in dose to OARs across all patients. For this reason, critical OARs exhibiting high variability and null dose in some patients such as the heart, esophagus, spinal cord and brachial plexus were excluded from the analysis. Finally, patient dose calculation/optimization was performed on the 4DCT average and not on individual respiratory phase-sorted images, which could yield variations in the reported results. Future work integrating robust MC optimization under perturbation of intra-fraction tumor motion, by calculating four-dimensional MC dose distributions (22) on time-weighted phases of the 4DCT while accounting for PBS respiratory-synchronized delivery timing, could prove valuable in improving lung proton therapy safety and efficacy. Finally, it should be noted that all clinical data to date published in proton beam radiotherapy for lung cancer have utilized PB algorithms and thus far a decrement in local control with protons relative to photons has not been observed (23,24).
Conclusions
A retrospective analysis of lung cancer patient PBS treatment plans demonstrated deficiencies in target coverage under PB planning with MC dosimetry, which were successfully resolved under MC planning. Robust optimization with MC planning had reduced sensitivity to range and setup perturbations compared to robust optimization with PB planning. In light of these findings, we strongly advocate for the widespread clinical adoption of MC-based treatment planning of lung cancer patients receiving scanned proton beam therapy.
Acknowledgements
We thank the dosimetry staff at the SCCA Proton Therapy Center for their efforts in initializing the original clinical planning parameters and configuration settings.
Funding: This work was partially supported by funding from NIH/NCI R01CA204301
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
Ethical Statement: This work was approved by the Institutional Review Board at the University of Washington (No. 9599).
References
- Liu H, Chang JY. Proton therapy in clinical practice. Chin J Cancer 2011;30:315-26. [Crossref] [PubMed]
- Kang M, Huang S, Solberg TD, et al. A study of the beam-specific interplay effect in proton pencil beam scanning delivery in lung cancer. Acta Oncol 2017;56:531-40. [Crossref] [PubMed]
- Dowdell S, Grassberger C, Sharp GC, et al. Interplay effects in proton scanning for lung: a 4D Monte Carlo study assessing the impact of tumor and beam delivery parameters. Phys Med Biol 2013;58:4137-56. [Crossref] [PubMed]
- Botas P, Grassberger C, Sharp G, et al. Density overwrites of internal tumor volumes in intensity modulated proton therapy plans for mobile lung tumors. Phys Med Biol 2018;63:035023. [Crossref] [PubMed]
- Soukup M, Fippel M, Alber M. A pencil beam algorithm for intensity modulated proton therapy derived from Monte Carlo simulations. Phys Med Biol 2005;50:5089-104. [Crossref] [PubMed]
- Hong L, Goitein M, Bucciolini M, et al. A pencil beam algorithm for proton dose calculations. Phys Med Biol 1996;41:1305-30. [Crossref] [PubMed]
- Schaffner B, Pedroni E, Lomax A. Dose calculation models for proton treatment planning using a dynamic beam delivery system: an attempt to include density heterogeneity effects in the analytical dose calculation. Phys Med Biol 1999;44:27-41. [Crossref] [PubMed]
- Grassberger C, Daartz J, Dowdell S, et al. Quantification of proton dose calculation accuracy in the lung. Int J Radiat Oncol Biol Phys 2014;89:424-30. [Crossref] [PubMed]
- Chen WZ, Xiao Y, Li J. Impact of dose calculation algorithm on radiation therapy. World J Radiol 2014;6:874-80. [Crossref] [PubMed]
- Saini J, Cao N, Bowen SR, et al. Clinical Commissioning of a Pencil Beam Scanning Treatment Planning System for Proton Therapy. Int J Part Ther 2016;3:51-60. [Crossref]
- Tourovsky A, Lomax AJ, Schneider U, et al. Monte Carlo dose calculations for spot scanned proton therapy. Phys Med Biol 2005;50:971-81. [Crossref] [PubMed]
- Bueno M, Paganetti H, Duch MA, et al. An algorithm to assess the need for clinical Monte Carlo dose calculation for small proton therapy fields based on quantification of tissue heterogeneity. Med Phys 2013;40:081704. [Crossref] [PubMed]
- Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys Med Biol 2012;57:R99-117. [Crossref] [PubMed]
- Paganetti H. Monte Carlo simulations will change the way we treat patients with proton beams today. Br J Radiol 2014;87:20140293. [Crossref] [PubMed]
- Taylor PA, Kry SF, Followill DS. Pencil Beam Algorithms Are Unsuitable for Proton Dose Calculations in Lung. Int J Radiat Oncol Biol Phys 2017;99:750-6. [Crossref] [PubMed]
- Saini J, Maes D, Egan A, et al. Dosimetric evaluation of a commercial proton spot scanning Monte-Carlo dose algorithm: comparisons against measurements and simulations. Phys Med Biol 2017;62:7659-81. [Crossref] [PubMed]
- Lee E, Zeng J, Miyaoka RS, et al. Functional lung avoidance and response-adaptive escalation (FLARE) RT: Multimodality plan dosimetry of a precision radiation oncology strategy. Med Phys 2017;44:3418-29. [Crossref] [PubMed]
- Bernatowicz K, Lomax AJ, Knopf A. Comparative study of layered and volumetric rescanning for different scanning speeds of proton beam in liver patients. Phys Med Biol 2013;58:7905-20. [Crossref] [PubMed]
- Lin L, Huang S, Kang M, et al. A benchmarking method to evaluate the accuracy of a commercial proton monte carlo pencil beam scanning treatment planning system. J Appl Clin Med Phys 2017;18:44-9. [Crossref] [PubMed]
- Schuemann J, Giantsoudi D, Grassberger C, et al. Assessing the Clinical Impact of Approximations in Analytical Dose Calculations for Proton Therapy. Int J Radiat Oncol Biol Phys 2015;92:1157-64. [Crossref] [PubMed]
- Schuemann J, Shin J, Perl J, et al. SU-E-T-500: Pencil-Beam versus Monte Carlo Based Dose Calculation for Proton Therapy Patients with Complex Geometries. Clinical Use of the TOPAS Monte Carlo System. Med Phys 2012;39:3820. [Crossref] [PubMed]
- Dowdell S, Grassberger C, Paganetti H. Four-dimensional Monte Carlo simulations demonstrating how the extent of intensity-modulation impacts motion effects in proton therapy lung treatments. Med Phys 2013;40:121713. [Crossref] [PubMed]
- Chang JY, Verma V, Li M, et al. Proton Beam Radiotherapy and Concurrent Chemotherapy for Unresectable Stage III Non-Small Cell Lung Cancer: Final Results of a Phase 2 Study. JAMA Oncol 2017;3:e172032. [Crossref] [PubMed]
- Liao Z, Lee JJ, Komaki R, et al. Bayesian Adaptive Randomization Trial of Passive Scattering Proton Therapy and Intensity-Modulated Photon Radiotherapy for Locally Advanced Non-Small-Cell Lung Cancer. J Clin Oncol 2018.JCO2017740720. [PubMed]


